javascript-algorithms
Detect Cycle in Graphs
In graph theory, a cycle is a path of edges and vertices wherein a vertex is reachable from itself. There are several different types of cycles, principally a closed walk and a simple cycle.
Definitions
A closed walk consists of a sequence of vertices starting and ending at the same vertex, with each two consecutive vertices in the sequence adjacent to each other in the graph. In a directed graph, each edge must be traversed by the walk consistently with its direction: the edge must be oriented from the earlier of two consecutive vertices to the later of the two vertices in the sequence. The choice of starting vertex is not important: traversing the same cyclic sequence of edges from different starting vertices produces the same closed walk.
A simple cycle may be defined either as a closed walk with no repetitions of vertices and edges allowed, other than the repetition of the starting and ending vertex, or as the set of edges in such a walk. The two definitions are equivalent in directed graphs, where simple cycles are also called directed cycles: the cyclic sequence of vertices and edges in a walk is completely determined by the set of edges that it uses. In undirected graphs the set of edges of a cycle can be traversed by a walk in either of two directions, giving two possible directed cycles for every undirected cycle. A circuit can be a closed walk allowing repetitions of vertices but not edges; however, it can also be a simple cycle, so explicit definition is recommended when it is used.
Example

A graph with edges colored to illustrate path H-A-B (green), closed path or
walk with a repeated vertex B-D-E-F-D-C-B (blue) and a cycle with no repeated edge or
vertex H-D-G-H (red)
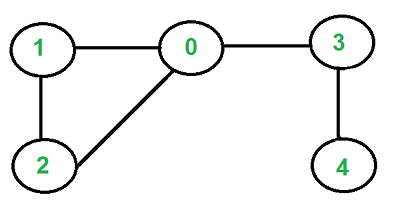
Cycle in undirected graph
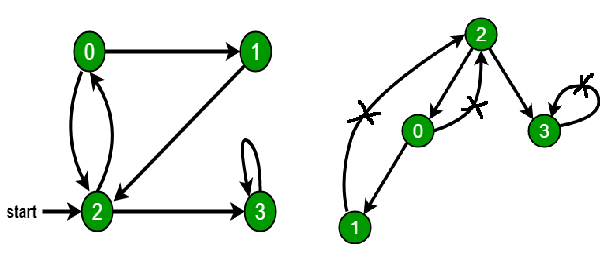
Cycle in directed graph
References
General information:
Cycles in undirected graphs:
- Detect Cycle in Undirected Graph on GeeksForGeeks
- Detect Cycle in Undirected Graph Algorithm on YouTube
Cycles in directed graphs: