javascript-algorithms

Levenshtein Distance

The Levenshtein distance is a string metric for measuring the difference between two sequences. Informally, the Levenshtein distance between two words is the minimum number of single-character edits (insertions, deletions or substitutions) required to change one word into the other.

Definition

Mathematically, the Levenshtein distance between two strings a and b (of length |a| and |b| respectively) is given by $Levenshtein$ where

$Levenshtein$

where $Levenshtein$ is the indicator function equal to 0 when $Levenshtein$ and equal to 1 otherwise, and $Levenshtein$ is the distance between the first i characters of a and the first j characters of b.

Note that the first element in the minimum corresponds to deletion (from a to b), the second to insertion and the third to match or mismatch, depending on whether the respective symbols are the same.

Example

For example, the Levenshtein distance between kitten and sitting is 3, since the following three edits change one into the other, and there is no way to do it with fewer than three edits:

kitten → sitten (substitution of “s” for “k”)
sitten → sittin (substitution of “i” for “e”)
sittin → sitting (insertion of “g” at the end).

Applications

This has a wide range of applications, for instance, spell checkers, correction systems for optical character recognition, fuzzy string searching, and software to assist natural language translation based on translation memory.

Dynamic Programming Approach Explanation

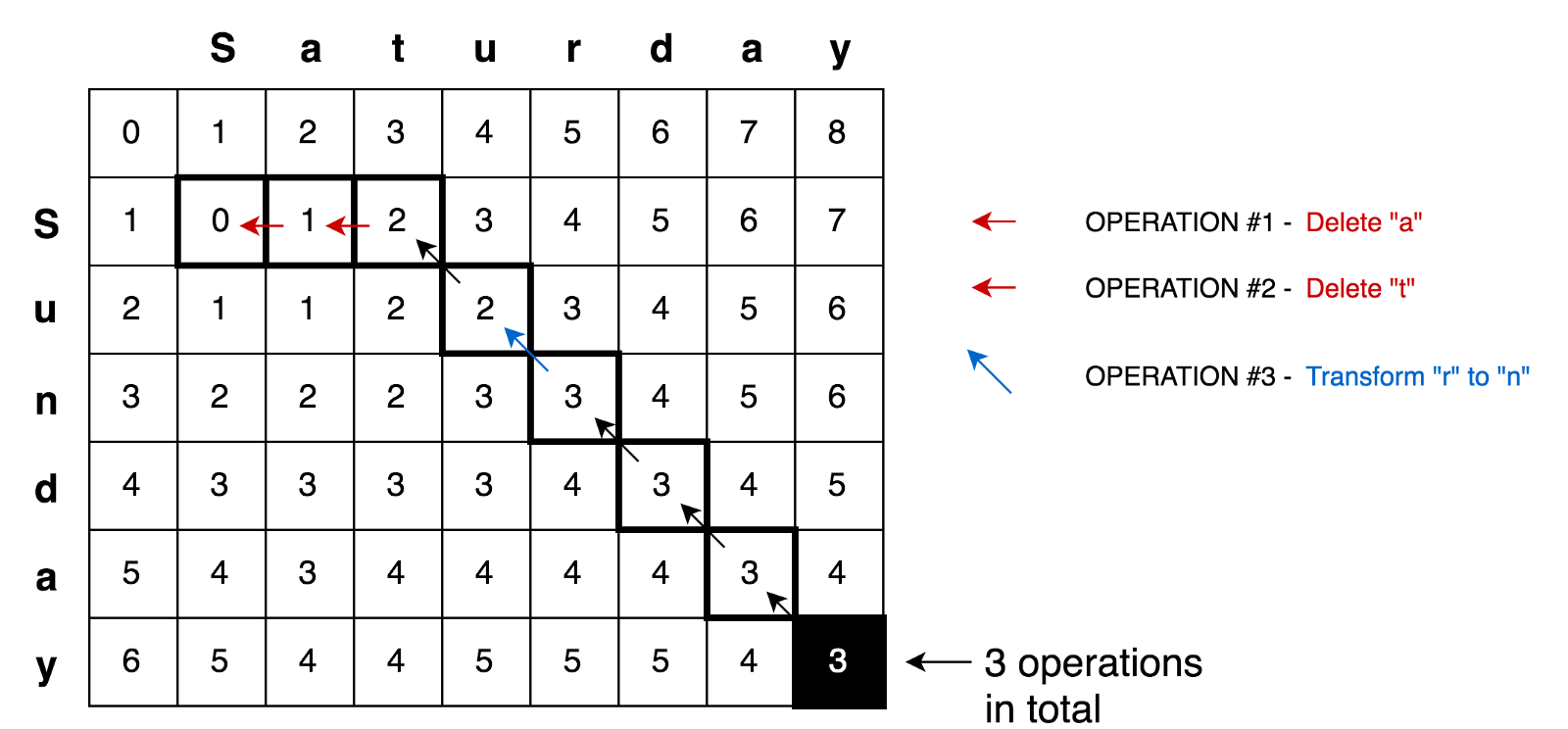
Let’s take a simple example of finding minimum edit distance between strings ME and MY. Intuitively you already know that minimum edit distance here is 1 operation and this operation. And it is replacing E with Y. But let’s try to formalize it in a form of the algorithm in order to be able to do more complex examples like transforming Saturday into Sunday.

To apply the mathematical formula mentioned above to ME → MY transformation we need to know minimum edit distances of ME → M, M → MY and M → M transformations in prior. Then we will need to pick the minimum one and add one operation to transform last letters E → Y. So minimum edit distance of ME → MY transformation is being calculated based on three previously possible transformations.

To explain this further let’s draw the following matrix:

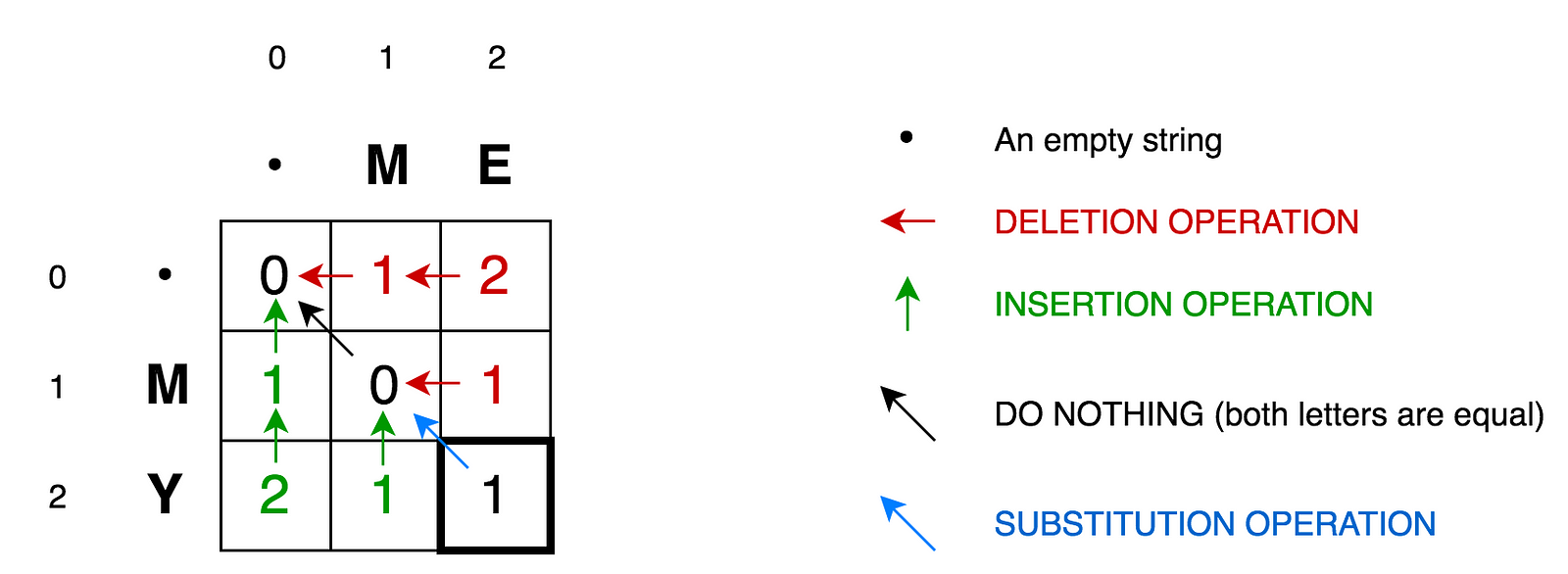
Levenshtein Matrix

Cell (0:1) contains red number 1. It means that we need 1 operation to transform M to an empty string. And it is by deleting M. This is why this number is red.
Cell (0:2) contains red number 2. It means that we need 2 operations to transform ME to an empty string. And it is by deleting E and M.
Cell (1:0) contains green number 1. It means that we need 1 operation to transform an empty string to M. And it is by inserting M. This is why this number is green.
Cell (2:0) contains green number 2. It means that we need 2 operations to transform an empty string to MY. And it is by inserting Y and M.
Cell (1:1) contains number 0. It means that it costs nothing to transform M into M.
Cell (1:2) contains red number 1. It means that we need 1 operation to transform ME to M. And it is by deleting E.
And so on…

This looks easy for such small matrix as ours (it is only 3x3). But here you may find basic concepts that may be applied to calculate all those numbers for bigger matrices (let’s say a 9x7 matrix for Saturday → Sunday transformation).

According to the formula you only need three adjacent cells (i-1:j), (i-1:j-1), and (i:j-1) to calculate the number for current cell (i:j). All we need to do is to find the minimum of those three cells and then add 1 in case if we have different letters in i’s row and j’s column.

You may clearly see the recursive nature of the problem.

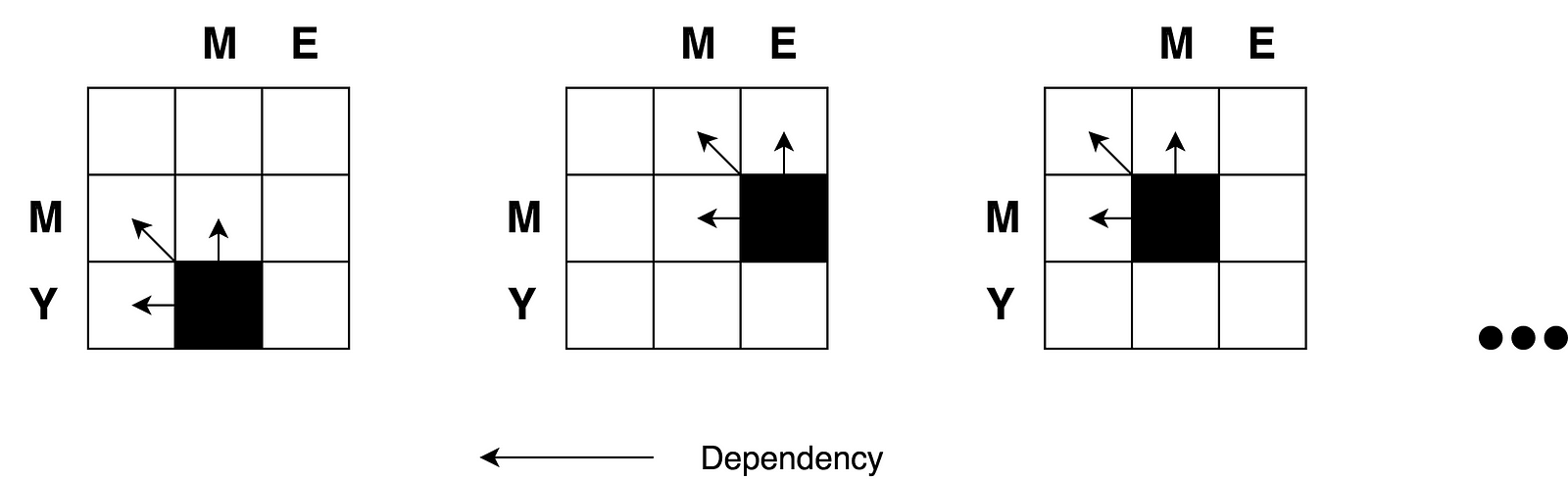
Levenshtein Matrix

Let’s draw a decision graph for this problem.

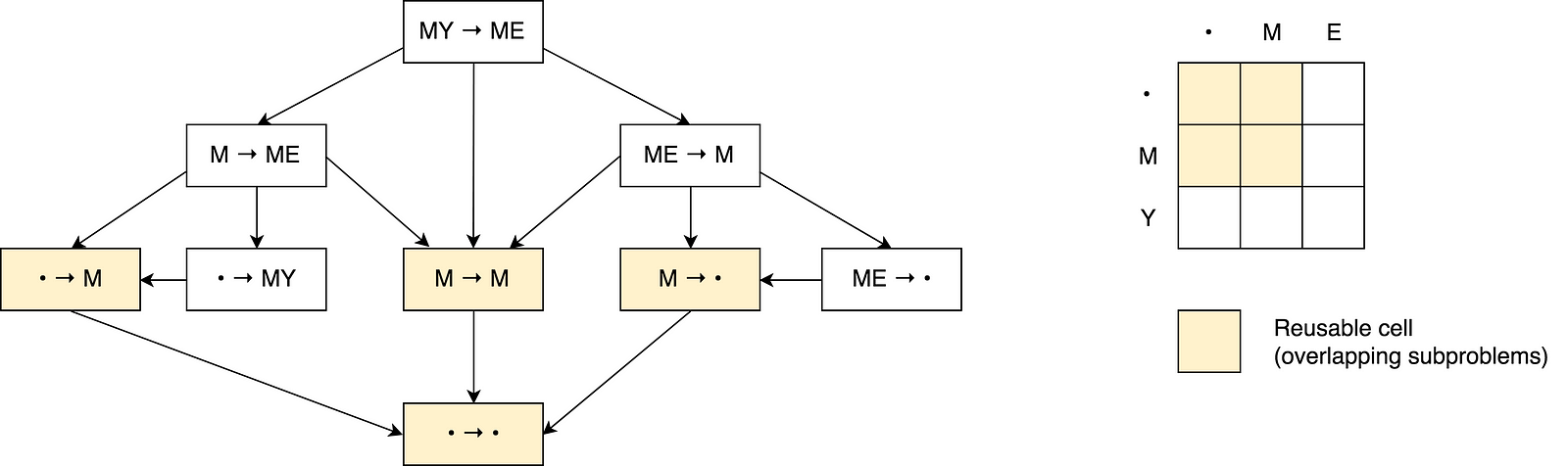
Minimum Edit Distance Decision Graph

You may see a number of overlapping sub-problems on the picture that are marked with red. Also there is no way to reduce the number of operations and make it less than a minimum of those three adjacent cells from the formula.

Also you may notice that each cell number in the matrix is being calculated based on previous ones. Thus the tabulation technique (filling the cache in bottom-up direction) is being applied here.

Applying this principle further we may solve more complicated cases like with Saturday → Sunday transformation.

Levenshtein distance

References

This site is open source. Improve this page.