javascript-algorithms
Árvore de Segmento (Segment Tree)
Na ciência da computação, uma árvore de segmento também conhecida como árvore estatística é uma árvore de estrutura de dados utilizadas para armazenar informações sobre intervalores ou segmentos. Ela permite pesquisas no qual os segmentos armazenados contém um ponto fornecido. Isto é, em princípio, uma estrutura estática; ou seja, é uma estrutura que não pode ser modificada depois de inicializada. Uma estrutura de dados similar é a árvore de intervalos.
Uma árvore de segmento é uma árvore binária. A raíz da árvore representa a array inteira. Os dois filhos da raíz representam a primeira e a segunda metade da array. Similarmente, os filhos de cada nó correspondem ao número das duas metadas da array correspondente do nó.
Nós construímos a árvore debaixo para cima, com o valor de cada nó sendo o
“mínimo” (ou qualquer outra função) dos valores de seus filhos. Isto consumirá
tempo O(n log n). O número de oprações realizadas é equivalente a altura da
árvore, pela qual consome tempo O(log n). Para fazer consultas de intervalos,
cada nó divide a consulta em duas partes, sendo uma sub consulta para cada filho.
Se uma pesquisa contém todo o subarray de um nó, nós podemos utilizar do valor
pré-calculado do nó. Utilizando esta otimização, nós podemos provar que somente
operações mínimas O(log n) são realizadas.
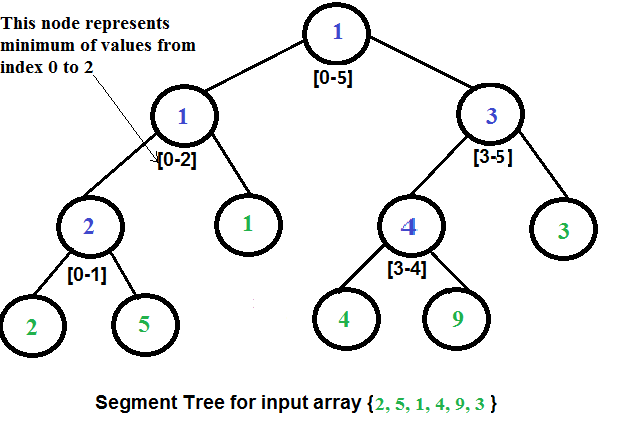
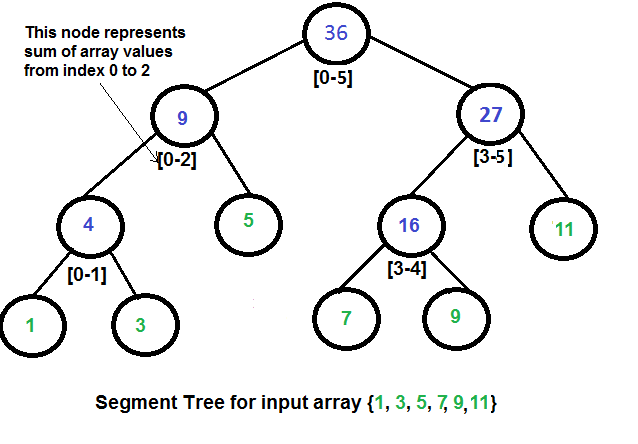
Aplicação
Uma árvore de segmento é uma estrutura de dados designada a realizar certas operações de array eficientemente, especialmente aquelas envolvendo consultas de intervalos.
Aplicações da árvore de segmentos são nas áreas de computação geométrica e sistemas de informação geográficos.
A implementação atual da Árvore de Segmentos implica que você pode passar
qualquer função binária (com dois parâmetros de entradas) e então, você
será capaz de realizar consultas de intervalos para uma variedade de funções.
Nos testes você poderá encontrar exemplos realizando min, max e consultas de
intervalo sum na árvore segmentada (SegmentTree).