javascript-algorithms

Algoritmos y Estructuras de Datos en JavaScript

Este repositorio contiene ejemplos basados en JavaScript de muchos algoritmos y estructuras de datos populares.

Cada algoritmo y estructura de datos tiene su propio LÉAME con explicaciones relacionadas y enlaces para lecturas adicionales (incluyendo algunas a vídeos de YouTube).

Léelo en otros idiomas: English, 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Português, Русский, Türk, Italiana

☝ Nótese que este proyecto está pensado con fines de aprendizaje e investigación, y no para ser usado en producción.

Estructuras de Datos

Una estructura de datos es una forma particular de organizar y almacenar datos en un ordenador para que puedan accederse y modificarse de forma eficiente. Más concretamente, una estructura de datos es un conjunto de valores de datos, las relaciones entre ellos y las funciones u operaciones que se pueden aplicar a los datos.

P - Principiante, A - Avanzado

P Lista enlazada
P Lista doblemente enlazada
P Cola
P Pila
P Tabla hash
P Heap - versiones máx y mín
P Cola de prioridad
A Trie
A Árbol
- A Árbol de búsqueda binaria
- A Árbol AVL
- A Árbol Rojo-Negro
- A Árbol de segmentos - con ejemplos de consultas de rango mín/máx/suma
- A Árbol de Fenwick (Árbol binario indexado)
A Grafo (dirigido y no dirigido)
A Conjuntos disjuntos
A Filtro de Bloom

Algoritmos

Un algoritmo es una especificación inequívoca de cómo resolver una clase de problemas. Es un conjunto de reglas que definen con precisión una secuencia de operaciones.

P - Principiante, A - Avanzado

Algoritmos por Tema

Matemáticas
- P Manipulación de bits - asignar/obtener/actualizar/limpiar bits, multiplicación/división por dos, hacer negativo, etc.
- P Factorial
- P Número de Fibonacci
- P Prueba de primalidad (método de división de prueba)
- P Algoritmo de Euclides - calcular el Máximo común divisor (MCD)
- P Mínimo común múltiplo (MCM)
- P Criba de Eratóstenes - encontrar todos los números primos hasta un límite dado
- P Es una potencia de dos? - comprobar si el número es una potencia de dos (algoritmos ingenuos y de bits)
- P Triángulo de Pascal
- P Números complejos - números complejos y operaciones con ellos
- P Radianes & Grados - conversión de radianes a grados y viceversa
- P Exponenciación rápida
- A Partición entera
- A Algortimo π de Liu Hui - aproximar el cálculo de π basado en polígonos de N lados
- A Transformada discreta de Fourier - descomponer una función de tiempo (señal) en las frecuencias que la componen
Conjuntos
- P Producto cartesiano - producto de múltiples conjuntos
- P Permutación de Fisher–Yates - permutación aleatoria de una secuencia finita
- A Conjunto potencia - todos los subconjuntos de un conjunto
- A Permutaciones (con y sin repeticiones)
- A Combinaciones (con y sin repeticiones)
- A Subsecuencia común más larga (LCS)
- A Subsecuencia creciente más larga
- A Supersecuencia común más corta (SCS)
- A Problema de la mochila - “0/1” y “sin límite”
- A Máximo subarreglo - versiones de “fuerza bruta” y “programación dinámica” (de Kadane)
- A Suma combinada - encuentra todas las combinaciones que forman una suma específica
Cadenas de caracteres
- P Distancia de Hamming - número de posiciones en las que los símbolos son diferentes
- A Distancia de Levenshtein - distancia mínima de edición entre dos secuencias
- A Algoritmo Knuth-Morris-Pratt (Algoritmo KMP) - búsqueda de subcadenas (coincidencia de patrones)
- A Algoritmo Z - búsqueda de subcadenas (coincidencia de patrones)
- A Algoritmo de Rabin Karp - búsqueda de subcadenas
- A Subcadena común más larga
- A Coincidencia por expresiones regulares
Búsquedas
- P Búsqueda lineal
- P Búsqueda de salto (o Búsqueda de bloque) - búsqueda en una lista ordenada
- P Búsqueda binaria - búsqueda en una lista ordenada
- P Búsqueda por interpolación - búsqueda en una lista ordenada uniformemente distribuida
Ordenamiento
- P Ordenamiento de burbuja
- P Ordenamiento por selección
- P Ordenamiento por inserción
- P Ordenamiento por Heap
- P Ordenamiento por mezcla
- P Quicksort - implementaciones in situ y no in situ
- P Shellsort
- P Ordenamiento por cuentas
- P Ordenamiento Radix
Listas enlazadas
- P Recorrido directo
- P Recorrido inverso
Árboles
- P Búsqueda en profundidad (DFS)
- P Búsqueda en anchura (BFS)
Grafos
- P Búsqueda en profundidad (DFS)
- P Búsqueda en anchura (BFS)
- P Algoritmo de Kruskal - encontrar el árbol de cubrimiento mínimo (MST) para un grafo no dirigido ponderado
- A Algoritmo de Dijkstra - encontrar los caminos más cortos a todos los vértices del grafo desde un solo vértice
- A Algoritmo de Bellman-Ford - encontrar los caminos más cortos a todos los vértices del grafo desde un solo vértice
- A Algortimo de Floyd-Warshall - encontrar los caminos más cortos entre todos los pares de vértices
- A Detectar ciclos - para grafos dirigidos y no dirigidos (versiones basadas en DFS y conjuntos disjuntos)
- A Algoritmo de Prim - encontrar el árbol de cubrimiento mínimo (MST) para un grafo no dirigido ponderado
- A Ordenamiento topológico - método DFS
- A Puntos de articulación - algoritmo de Tarjan (basado en DFS)
- A Puentes - algoritmo basado en DFS
- A Camino euleriano y circuito euleriano - algoritmo de Fleury - visitar cada arista exactamente una vez
- A Ciclo hamiltoniano - visitar cada vértice exactamente una vez
- A Componentes fuertemente conexos - algoritmo de Kosaraju
- A Problema del viajante - la ruta más corta posible que visita cada ciudad y vuelve a la ciudad de origen
Criptografia
- P Hash polinomial - función de hash rodante basada en polinomio
Sin categoría
- P Torre de Hanói
- P Rotación de matriz cuadrada - algoritmo in situ
- P Juego de los saltos - ejemplos de backtracking, programación dinámica (de arriba hacia abajo + de abajo hacia arriba) y voraces
- P Caminos únicos - ejemplos de backtracking, programación dinámica y basados en el Triángulo de Pascal
- P Terrazas pluviales - el problema de la retención del agua de lluvia (programación dinámica y fuerza bruta)
- A Problema de las N Reinas
- A Problema del caballo (Knight tour)

Algoritmos por paradigma

Un paradigma algorítmico es un método o enfoque genérico que subyace al diseño de una clase de algoritmos. Es una abstracción superior a la noción de algoritmo, del mismo modo que un algoritmo es una abstracción superior a un programa de ordenador.

Fuerza Bruta - mira todas las posibilidades y selecciona la mejor solución
- P Búsqueda lineal
- P Terrazas pluviales - el problema de la retención del agua de lluvia
- A Máximo subarreglo
- A Problema del viajante - la ruta más corta posible que visita cada ciudad y vuelve a la ciudad de origen
- A Transformada discreta de Fourier - descomponer una función de tiempo (señal) en las frecuencias que la componen
Voraces - escoge la mejor opción en el momento actual, sin ninguna consideración sobre el futuro
- P Juego de los saltos
- A Problema de la mochila sin límite
- A Algoritmo de Dijkstra - encontrar los caminos más cortos a todos los vértices del grafo desde un solo vértice
- A Algortimo de Prim - encontrar el árbol de cubrimiento mínimo (MST) para un grafo no dirigido ponderado
- A Algoritmo de Kruskal - encontrar el árbol de cubrimiento mínimo (MST) para un grafo no dirigido ponderado
Divide y Vencerás - divide el problema en partes más pequeñas y luego resuelve esas partes
- P Búsqueda binaria
- P Torre de Hanói
- P Triángulo de Pascal
- P Algoritmo de Euclides - calcular el Máximo Común Divisor (MCD)
- P Ordenamiento por mezcla
- P Quicksort
- P Búsqueda en profundidad (árboles) - (DFS)
- P Búsqueda en profundidad (grafos) - (DFS)
- P Juego de los saltos
- P Exponenciación rápida
- A Permutaciones - (con y sin repeticiones)
- A Combinaciones - (con y sin repeticiones)
Programación Dinámica - construye una solución usando sub-soluciones previamente encontradas
- P Número de Fibonacci
- P Juego de los saltos
- P Caminos únicos
- P Terrazas pluviales - el problema de la retención del agua de lluvia
- A Distancia de Levenshtein - distancia mínima de edición entre dos secuencias
- A Subsecuencia común más larga (LCS)
- A Subcadena común más larga
- A Subsecuencia creciente más larga
- A Supersecuencia común más corta
- A Problema de la mochila 0/1
- A Partición entera
- A Máximo subarreglo
- A Algoritmo de Bellman-Ford - encontrar los caminos más cortos a todos los vértices del grafo desde un solo vértice
- A Algoritmo de Floyd-Warshall - encontrar los caminos más cortos entre todos los pares de vértices
- A Coincidencia por expresiones regulares
De Retorceso (Backtracking) - De manera similar a la fuerza bruta, trata de generar todas las soluciones posibles, pero cada vez que genere la siguiente solución, comprueba si cumple con todas las condiciones, y sólo entonces continúa generando soluciones posteriores. De lo contrario, retrocede y sigue un camino diferente para encontrar una solución. Normalmente se utiliza un recorrido en profundidad (DFS) del espacio de estados.
- P Juego de los saltos
- P Caminos únicos
- P Conjunto potencia - todos los subconjuntos de un conjunto
- A Ciclo hamiltoniano - visitar cada vértice exactamente una vez
- A Problema de las N Reinas
- A Problema del caballo (Knight tour)
- A Suma combinada - encuentra todas las combinaciones que forman una suma específica
Ramas y Limites - recuerda la solución de menor costo encontrada en cada etapa de la búsqueda de rastreo, y utilizar el costo de la solución de menor costo encontrada hasta el momento como un límite inferior del costo de una solución de menor costo para el problema, a fin de descartar soluciones parciales con costos mayores que la solución de menor costo encontrada hasta el momento. Normalmente se utiliza un recorrido BFS en combinación con un recorrido DFS del árbol del espacio de estados.

Cómo usar este repositorio

Instalar las dependencias

npm install

Correr ESLint

Es posible que desee ejecutarlo para comprobar la calidad del código.

npm run lint

Correr los tests

npm test

Correr tests por nombre

npm test -- 'LinkedList'

Campo de juegos

Puede jugar con estructuras de datos y algoritmos en el archivo ./src/playground/playground.js y escribir pruebas para ello en ./src/playground/__test__/playground.test.js.

A continuación, simplemente ejecute el siguiente comando para comprobar si el código funciona como se espera:

npm test -- 'playground'

Información útil

Refrencias

▶ Estructuras de datos y algoritmos en YouTube

Notación O Grande

Orden de crecimiento de los algoritmos especificados en la notación O grande.

Gráficas de Notación O grande

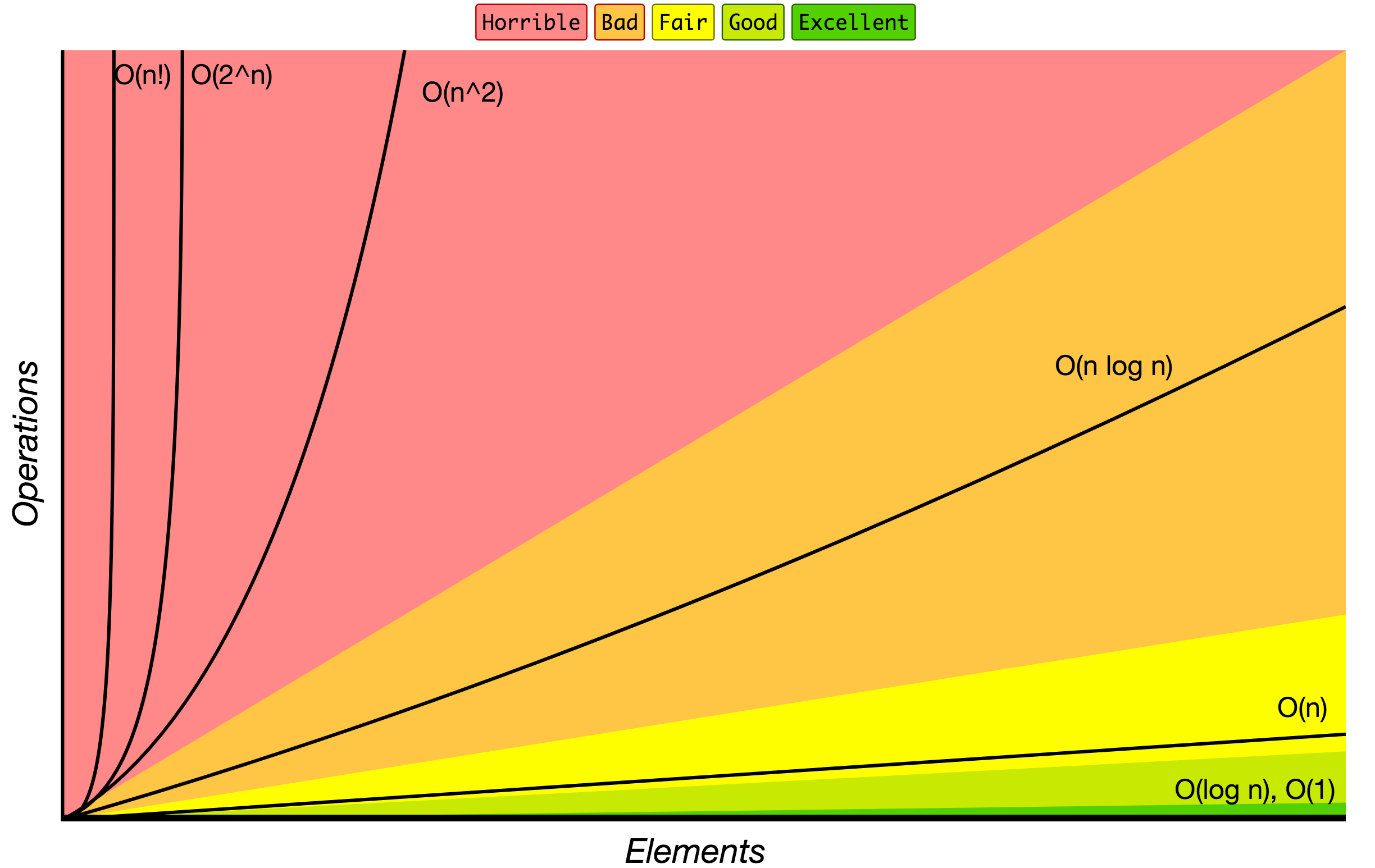
Fuente: Big O Cheat Sheet.

A continuación se muestra la lista de algunas de las notaciones de Big O más utilizadas y sus comparaciones de rendimiento frente a diferentes tamaños de los datos de entrada.

Notación O grande	Cálculos para 10 elementos	Cálculos para 100 elementos	Cálculos para 1000 elementos
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

Complejidad de las operaciones de estructuras de datos

Estructura de Datos	Accesso	Busqueda	Inserción	Borrado	Comentarios
Colección	1	n	n	n
Stack	n	n	1	1
Cola	n	n	1	1
Lista enlazada	n	n	1	1
Tabla hash	-	n	n	n	En caso de función hash perfecta los costos serían O(1)
Búsqueda por Árbol binario	n	n	n	n	En el caso de un árbol equilibrado, los costos serían O(log(n))
Árbol B	log(n)	log(n)	log(n)	log(n)
Árbol Rojo-Negro	log(n)	log(n)	log(n)	log(n)
Árbol AVL	log(n)	log(n)	log(n)	log(n)
Filtro de Bloom	-	1	1	-	Falsos positivos son posibles durante la búsqueda

Complejidad de algoritmos de ordenamiento de arreglos

Nombre	Mejor	Promedio	Pero	Memorya	Estable	Comentarios
Ordenamiento de burbuja	n	n²	n²	1	Si
Ordenamiento por inserción	n	n²	n²	1	Si
Ordenamiento por selección	n²	n²	n²	1	No
Ordenamiento por Heap	n log(n)	n log(n)	n log(n)	1	No
Ordenamiento por mezcla	n log(n)	n log(n)	n log(n)	n	Si
Quicksort	n log(n)	n log(n)	n²	log(n)	No	Quicksort utiliza O(log(n)) de espacio en el stack
Shellsort	n log(n)	depende de la secuencia de huecos	n (log(n))²	1	No
Ordenamiento por cuentas	n + r	n + r	n + r	n + r	Si	r - mayor número en el arreglo
Ordenamiento Radix	n * k	n * k	n * k	n + k	Si	k - largo de la llave más larga

This site is open source. Improve this page.