javascript-algorithms

Algorithmes et Structures de Données en JavaScript

Ce dépôt contient des exemples d’implémentation en JavaScript de plusieurs algorithmes et structures de données populaires.

Chaque algorithme et structure de donnée possède son propre README contenant les explications détaillées et liens (incluant aussi des vidéos Youtube) pour complément d’informations.

Lisez ceci dans d’autres langues: English, 简体中文, 繁體中文, 한국어, 日本語, Polski, Español, Português, Русский, Türk, Italiana

Data Structures

Une structure de données est une manière spéciale d’organiser et de stocker des données dans un ordinateur de manière à ce que l’on puisse accéder à cette information et la modifier de manière efficiente. De manière plus spécifique, une structure de données est un ensemble composé d’une collection de valeurs, des relations entre ces valeurs ainsi que d’un ensemble de fonctions ou d’opérations pouvant être appliquées sur ces données.

B - Débutant, A - Avancé

• B Liste Chaînée
• B Liste Doublement Chaînée
• B Queue
• B Pile
• B Table de Hachage
• B Tas
• B Queue de Priorité
• A Trie
• A Arbre
  • A Arbre de recherche Binaire
  • A Arbre AVL
  • A Arbre Red-Black
  • A Arbre de Segments - avec exemples de requêtes de type min/max/somme sur intervalles
  • A Arbre de Fenwick (Arbre Binaire Indexé)
• A Graphe (orienté et non orienté)
• A Ensembles Disjoints
• A Filtre de Bloom

Algorithmes

Un algorithme est une démarche non ambigüe expliquant comment résoudre une classe de problèmes. C’est un ensemble de règles décrivant de manière précise une séquence d’opérations.

B - Débutant, A - Avancé

Algorithmes par topic

• Math
  • B Manipulation de Bit - définir/obtenir/mettre à jour/effacer les bits, multiplication/division par deux, négativiser etc.
  • B Factorielle
  • B Nombre de Fibonacci
  • B Test de Primalité (méthode du test de division)
  • B Algorithme d’Euclide - calcule le Plus Grand Commun Diviseur (PGCD)
  • B Plus Petit Commun Multiple (PPCM)
  • B Crible d’Eratosthène - trouve tous les nombres premiers inférieurs à une certaine limite
  • B Puissance de Deux - teste si un nombre donné est une puissance de deux (algorithmes naif et basé sur les opérations bit-à-bit)
  • B Triangle de Pascal
  • B Nombre complexe - nombres complexes et opérations de bases
  • A Partition Entière
  • A Approximation de π par l’algorithme de Liu Hui - approximation du calcul de π basé sur les N-gons
  • B Exponentiation rapide
  • A Transformée de Fourier Discrète - décomposer une fonction du temps (un signal) en fréquences qui la composent
• Ensembles
  • B Produit Cartésien - produit de plusieurs ensembles
  • B Mélange de Fisher–Yates - permulation aléatoire d’une séquence finie
  • A Ensemble des parties d’un ensemble - tous les sous-ensembles d’un ensemble
  • A Permutations (avec et sans répétitions)
  • A Combinaisons (avec et sans répétitions)
  • A Plus Longue Sous-séquence Commune
  • A Plus Longue Sous-suite strictement croissante
  • A Plus Courte Super-séquence Commune
  • A Problème du Sac à Dos - versions “0/1” et “Sans Contraintes”
  • A Sous-partie Maximum - versions “Force Brute” et “Programmation Dynamique” (Kadane)
  • A Somme combinatoire - trouve toutes les combinaisons qui forment une somme spécifique
• Chaînes de Caractères
  • B Distance de Hamming - nombre de positions auxquelles les symboles sont différents
  • A Distance de Levenshtein - distance minimale d’édition entre deux séquences
  • A Algorithme de Knuth–Morris–Pratt (Algorithme KMP) - recherche de sous-chaîne (pattern matching)
  • A Algorithme Z - recherche de sous-chaîne (pattern matching)
  • A Algorithme de Rabin Karp - recherche de sous-chaîne
  • A Plus Longue Sous-chaîne Commune
  • A Expression Régulière
• Recherche
  • B Recherche Linéaire
  • B Jump Search Recherche par saut (ou par bloc) - recherche dans une liste triée
  • B Recherche Binaire - recherche dans une liste triée
  • B Recherche par Interpolation - recherche dans une liste triée et uniformément distribuée
• Tri
  • B Tri Bullet
  • B Tri Sélection
  • B Tri Insertion
  • B Tri Par Tas
  • B Tri Fusion
  • B Tri Rapide - implémentations in-place et non in-place
  • B Tri Shell
  • B Tri Comptage
  • B Tri Radix
• Arbres
  • B Parcours en Profondeur (DFS)
  • B Parcours en Largeur (BFS)
• Graphes
  • B Parcours en Profondeur (DFS)
  • B Parcours en Largeur (BFS)
  • B Algorithme de Kruskal - trouver l’arbre couvrant de poids minimal sur un graphe pondéré non dirigé
  • A Algorithme de Dijkstra - trouver tous les plus courts chemins partant d’un noeud vers tous les autres noeuds dans un graphe
  • A Algorithme de Bellman-Ford - trouver tous les plus courts chemins partant d’un noeud vers tous les autres noeuds dans un graphe
  • A Algorithme de Floyd-Warshall - trouver tous les plus courts chemins entre toutes les paires de noeuds dans un graphe
  • A Détection de Cycle - pour les graphes dirigés et non dirigés (implémentations basées sur l’algorithme de Parcours en Profondeur et sur les Ensembles Disjoints)
  • A Algorithme de Prim - trouver l’arbre couvrant de poids minimal sur un graphe pondéré non dirigé
  • A Tri Topologique - méthode DFS
  • A Point d’Articulation - algorithme de Tarjan (basé sur l’algorithme de Parcours en Profondeur)
  • A Bridges - algorithme basé sur le Parcours en Profondeur
  • A Chemin Eulérien et Circuit Eulérien - algorithme de Fleury - visite chaque arc exactement une fois
  • A Cycle Hamiltonien - visite chaque noeud exactement une fois
  • A Composants Fortements Connexes - algorithme de Kosaraju
  • A Problème du Voyageur de Commerce - chemin le plus court visitant chaque cité et retournant à la cité d’origine
• Non catégorisé
  • B Tours de Hanoi
  • B Rotation de Matrice Carrée - algorithme in place
  • B Jump Game - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples gourmands
  • B Chemins Uniques - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples basés sur le Triangle de Pascal
  • A Problème des N-Dames
  • A Problème du Cavalier

Algorithmes par Paradigme

Un paradigme algorithmique est une méthode générique ou une approche qui sous-tend la conception d’une classe d’algorithmes. C’est une abstraction au-dessus de la notion d’algorithme, tout comme l’algorithme est une abstraction supérieure à un programme informatique.

• Force Brute - cherche parmi toutes les possibilités et retient la meilleure
  • B Recherche Linéaire
  • A Sous-partie Maximum
  • A Problème du Voyageur de Commerce - chemin le plus court visitant chaque cité et retournant à la cité d’origine
• Gourmand - choisit la meilleure option à l’instant courant, sans tenir compte de la situation future
  • B Jump Game
  • A Problème du Sac à Dos Sans Contraintes
  • A Algorithme de Dijkstra - trouver tous les plus courts chemins partant d’un noeud vers tous les autres noeuds dans un graphe
  • A Algorithme de Prim - trouver l’arbre couvrant de poids minimal sur un graphe pondéré non dirigé
  • A Algorithme de Kruskal - trouver l’arbre couvrant de poids minimal sur un graphe pondéré non dirigé
• Diviser et Régner - divise le problème en sous problèmes (plus simples) et résoud ces sous problèmes
  • B Recherche Binaire
  • B Tours de Hanoi
  • B Triangle de Pascal
  • B Algorithme d’Euclide - calcule le Plus Grand Commun Diviseur (PGCD)
  • B Tri Fusion
  • B Tri Rapide
  • B Arbre de Parcours en Profondeur (DFS)
  • B Graphe de Parcours en Profondeur (DFS)
  • B Jump Game
  • A Permutations (avec et sans répétitions)
  • A Combinations (avec et sans répétitions)
• Programmation Dynamique - construit une solution en utilisant les solutions précédemment trouvées
  • B Nombre de Fibonacci
  • B Jump Game
  • B Chemins Uniques
  • A Distance de Levenshtein - distance minimale d’édition entre deux séquences
  • A Plus Longue Sous-séquence Commune
  • A Plus Longue Sous-chaîne Commune
  • A Plus Longue Sous-suite strictement croissante
  • A Plus Courte Super-séquence Commune
  • A Problème de Sac à Dos
  • A Partition Entière
  • A Sous-partie Maximum
  • A Algorithme de Bellman-Ford - trouver tous les plus courts chemins partant d’un noeud vers tous les autres noeuds dans un graphe
  • A Algorithme de Floyd-Warshall - trouver tous les plus courts chemins entre toutes les paires de noeuds dans un graphe
  • A Expression Régulière
• Retour sur trace - de même que la version “Force Brute”, essaie de générer toutes les solutions possibles, mais pour chaque solution générée, on teste si elle satisfait toutes les conditions, et seulement ensuite continuer à générer des solutions ultérieures. Sinon, l’on revient en arrière, et l’on essaie un chemin différent pour tester d’autres solutions. Normalement, la traversée en profondeur de l’espace d’états est utilisée.
  • B Jump Game
  • B Unique Paths
  • A Hamiltonian Cycle - Visit every vertex exactly once
  • A Problème des N-Dames
  • A Problème du Cavalier
  • A Somme combinatoire - trouve toutes les combinaisons qui forment une somme spécifique
• Séparation et Evaluation - pemet de retenir une solution à moindre coût dans un ensemble. Pour chaque étape, l’on garde une trace de la solution la moins coûteuse trouvée jusqu’à présent en tant que borne inférieure du coût. Cela afin d’éliminer les solutions partielles dont les coûts sont plus élevés que celui de la solution actuelle retenue. Normalement, la traversée en largeur en combinaison avec la traversée en profondeur de l’espace d’états de l’arbre est utilisée.

Comment utiliser ce dépôt

Installer toutes les dépendances

npm install

Exécuter ESLint

Vous pouvez l’installer pour tester la qualité du code.

npm run lint

Exécuter tous les tests

npm test

Exécuter les tests par nom

npm test -- 'LinkedList'

Tests personnalisés

Vous pouvez manipuler les structures de données et algorithmes présents dans ce dépôt avec le fichier ./src/playground/playground.js et écrire vos propres tests dans file ./src/playground/__test__/playground.test.js.

Vous pourrez alors simplement exécuter la commande suivante afin de tester si votre code fonctionne comme escompté

npm test -- 'playground'

Informations Utiles

Références

▶ Structures de Données et Algorithmes sur YouTube

Notation Grand O

Comparaison de la performance d’algorithmes en notation Grand O.

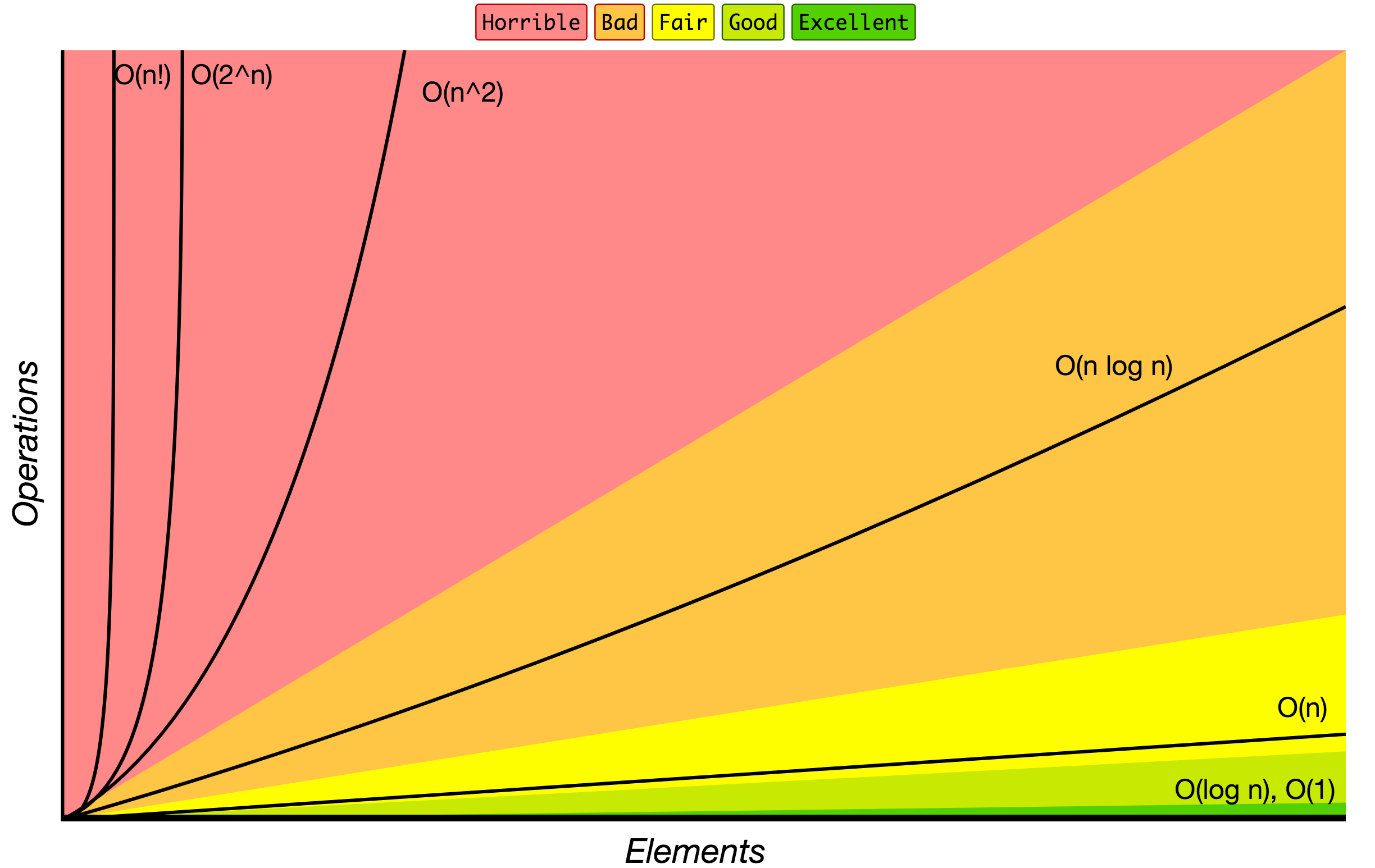
Source: Big O Cheat Sheet.

Voici la liste de certaines des notations Grand O les plus utilisées et de leurs comparaisons de performance suivant différentes tailles pour les données d’entrée.

Notation Grand O	Opérations pour 10 éléments	Opérations pour 100 éléments	Opérations pour 1000 éléments
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

Complexité des Opérations suivant les Structures de Données

Structure de donnée	Accès	Recherche	Insertion	Suppression	Commentaires
Liste	1	n	n	n
Pile	n	n	1	1
Queue	n	n	1	1
Liste Liée	n	n	1	1
Table de Hachage	-	n	n	n	Dans le cas des fonctions de hachage parfaites, les couts seraient de O(1)
Arbre de Recherche Binaire	n	n	n	n	Dans le cas des arbre équilibrés, les coûts seraient de O(log(n))
Arbre B	log(n)	log(n)	log(n)	log(n)
Arbre Red-Black	log(n)	log(n)	log(n)	log(n)
Arbre AVL	log(n)	log(n)	log(n)	log(n)
Filtre de Bloom	-	1	1	-	Les faux positifs sont possibles lors de la recherche

Complexité des Algorithmes de Tri de Liste

Nom	Meilleur	Moyenne	Pire	Mémoire	Stable	Commentaires
Tri Bulle	n	n2	n2	1	Oui
Tri Insertion	n	n2	n2	1	Oui
Tri Sélection	n2	n2	n2	1	Non
Tri par Tas	n log(n)	n log(n)	n log(n)	1	Non
Merge sort	n log(n)	n log(n)	n log(n)	n	Oui
Tri Rapide	n log(n)	n log(n)	n2	log(n)	Non	le Tri Rapide est généralement effectué in-place avec une pile de taille O(log(n))
Tri Shell	n log(n)	dépend du gap séquence	n (log(n))2	1	Non
Tri Comptage	n + r	n + r	n + r	n + r	Oui	r - le plus grand nombre dans la liste
Tri Radix	n * k	n * k	n * k	n + k	Non	k - longueur du plus long index

This site is open source. Improve this page.