javascript-algorithms

JavaScript Algoritmalar ve Veri Yapıları

Bu repository JavaScript’e ait popüler algoritma ve veri yapılarını içermektedir.

Her bir algoritma ve veri yapısı kendine ait açıklama ve videoya sahip README dosyası içerir.

Read this in other languages: 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español, Português, Русский, Italiana

☝ Not, bu proje araştırma ve öğrenme amacı ile yapılmış olup üretim için yaplılmamıştır.

Veri Yapıları

Bir veri yapısı, verileri bir bilgisayarda organize etmenin ve depolamanın belirli bir yoludur, böylece verimli bir şekilde erişilebilir ve değiştirilebilir. Daha doğrusu, bir veri yapısı bir veri koleksiyonudur, aralarındaki ilişkiler, ve işlevler veya işlemler veriye uygulanabilir.

B - Başlangıç, A - İleri Seviye

• B Bağlantılı Veri Yapısı
• B Çift Yönlü Bağlı Liste
• B Kuyruk
• B Yığın
• B Hash Table
• B Heap - max and min heap versions
• B Öncelikli Kuyruk
• A Trie
• A Ağaç
  • A İkili Arama Ağaçları
  • A AVL Tree
  • A Red-Black Tree
  • A Segment Tree - with min/max/sum range queries examples
  • A Fenwick Tree (Binary Indexed Tree)
• A Graph (both directed and undirected)
• A Disjoint Set
• A Bloom Filter

Algoritmalar

Bir algoritma, bir problem sınıfının nasıl çözüleceğine dair kesin bir tanımlamadır. Bu bir işlem dizisini kesin olarak tanımlayan bir dizi kural.

B - Başlangıç, A - İleri Seviye

Konusuna göre Algoritma

• Matematik
  • B Bit Manipülasyonu - set/get/update/clear bits, multiplication/division by two, make negative etc.
  • B Faktöriyel
  • B Fibonacci Sayısı - klasik ve kapalı-form versiyonları
  • B Asallık Testi (trial division method)
  • B Öklid Algoritması - En büyük ortak bölen hesaplama (EBOB)
  • B En küçük Ortak Kat (EKOK)
  • B Sieve of Eratosthenes - belirli bir sayıya kadarki asal sayıları bulma
  • B Is Power of Two - sayı ikinin katı mı sorgusu (naive ve bitwise algoritmaları)
  • B Paskal Üçgeni
  • B Karmaşık Sayılar - karmaşık sayılar ve bunlarla temel işlemler
  • B Radyan & Derece - radyandan dereceye çeviri ve tersi
  • B Fast Powering
  • A Tamsayı Bölümü
  • A Karekök - Newton yöntemi
  • A Liu Hui π Algoritması - N-gons’a göre yaklaşık π hesabı
  • A Ayrık Fourier Dönüşümü - bir zaman fonksiyonunu (bir sinyal) onu oluşturan frekanslara ayırır
• Setler
  • B Kartezyen Ürün - product of multiple sets
  • B Fisher–Yates Shuffle - sonlu bir dizinin rastgele permütasyonu
  • A Power Set - all subsets of a set (bitwise and backtracking solutions)
  • A Permütasyonlar(tekrarlı ve tekrarsız)
  • A Kombinasyonlar (tekrarlı ve tekrarsız)
  • A En Uzun Ortak Altdizi (LCS)
  • A En Uzun Artan Altdizi
  • A En Kısa Ortak Üst Sıra (SCS)
  • A Knapsack Problem - “0/1” and “Unbound” ones
  • A Maksimum Altdizi - “Brute Force” ve “Dinamik Programlara” (Kadane’nin) versiyonu
  • A Kombinasyon Toplamı - belirli toplamı oluşturan tüm kombinasyonları bulun
• Metin
  • B Hamming Mesafesi - sembollerin farklı olduğu konumların sayısı
  • A Levenshtein Mesafesi - iki sekans arasındaki minimum düzenleme mesafesi
  • A Knuth–Morris–Pratt Algoritması (KMP Algorithm) - substring search (pattern matching)
  • A Z Algoritması - altmetin araması (desen eşleştirme)
  • A Rabin Karp Algoritması - altmetin araması
  • A En Uzun Ortak Alt Metin
  • A Regular Expression Eşleme
• Aramalar
  • B Doğrusal Arama
  • B Jump Search (ya da Block Search) - sıralı dizide ara
  • B İkili Arama - sıralı dizide ara
  • B Interpolation Search - tekdüze dağıtılmış sıralı dizide arama
• Sıralama
  • B Bubble Sort
  • B Selection Sort
  • B Insertion Sort
  • B Heap Sort
  • B Merge Sort
  • B Quicksort - in-place and non-in-place implementations
  • B Shellsort
  • B Counting Sort
  • B Radix Sort
• Bağlantılı Liste
  • B Straight Traversal
  • B Reverse Traversal
• Ağaçlar
  • B Depth-First Search (DFS)
  • B Breadth-First Search (BFS)
• Graphs
  • B Depth-First Search (DFS)
  • B Breadth-First Search (BFS)
  • B Kruskal’s Algorithm - ağırlıklı yönlendirilmemiş grafik için Minimum Yayılma Ağacı’nı (MST) bulma
  • A Dijkstra Algorithm - tek tepe noktasından tüm grafik köşelerine en kısa yolları bulmak
  • A Bellman-Ford Algorithm - tek tepe noktasından tüm grafik köşelerine en kısa yolları bulmak
  • A Floyd-Warshall Algorithm - tüm köşe çiftleri arasındaki en kısa yolları bulun
  • A Detect Cycle - hem yönlendirilmiş hem de yönlendirilmemiş grafikler için (DFS ve Ayrık Küme tabanlı sürümler)
  • A Prim’s Algorithm - ağırlıklı yönlendirilmemiş grafik için Minimum Yayılma Ağacı’nı (MST) bulma
  • A Topological Sorting - DFS metodu
  • A Articulation Points - Tarjan’s algoritması (DFS based)
  • A Bridges - DFS yöntemi ile algoritma
  • A Eulerian Path and Eulerian Circuit - Fleury’nin algoritması - Her kenara tam olarak bir kez ulaş
  • A Hamiltonian Cycle - Her köşeyi tam olarak bir kez ziyaret et
  • A Strongly Connected Components - Kosaraju’s algorithm
  • A Travelling Salesman Problem - her şehri ziyaret eden ve başlangıç ​​şehrine geri dönen mümkün olan en kısa rota
• Kriptografi
  • B Polynomial Hash - polinom temelinde dönen hash işlevi
  • B Caesar Cipher - simple substitution cipher
• Makine Öğrenmesi
  • B NanoNeuron - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)
• Kategoriye Ayrılmayanlar
  • B Tower of Hanoi
  • B Square Matrix Rotation - in-place algorithm
  • B Jump Game - backtracking, dynamic programming (top-down + bottom-up) and greedy examples
  • B Unique Paths - backtracking, dynamic programming and Pascal’s Triangle based examples
  • B Rain Terraces - trapping rain water problem (dynamic programming and brute force versions)
  • B Recursive Staircase - tepeye ulaşmanın yollarını sayma (4 çözüm)
  • A N-Queens Problem
  • A Knight’s Tour

Algoritmik Paradigma

Algoritmik paradigma, bir sınıfın tasarımının altında yatan genel bir yöntem veya yaklaşımdır. Algoritma dizayn tekniği olarak düşünülebilir. Her bir altproblemi (subproblem) asıl problemle benzerlik gösteren problemlere uygulanabilir.

• Brute Force - mümkün olan tüm çözümleri tara ve en iyisini seç
  • B Doğrusal Arama
  • B Rain Terraces - trapping rain water problem
  • B Recursive Staircase - tepeye çıkmanın yollarını hesapla
  • A Maximum Subarray
  • A Travelling Salesman Problem - her şehri ziyaret eden ve başlangıç şehrine geri dönen mümkün olan en kısa rota
  • A Discrete Fourier Transform - bir zaman fonksiyonunu (bir sinyal) onu oluşturan frekanslara ayırır
• Açgözlü - geleceği düşünmeden şu an için en iyi seçeneği seçin
  • B Jump Game
  • A Unbound Knapsack Problem
  • A Dijkstra Algorithm - tüm grafik köşelerine giden en kısa yolu bulmak
  • A Prim’s Algorithm - ağırlıklı yönlendirilmemiş grafik için Minimum Yayılma Ağacı’nı (MST) bulma
  • A Kruskal’s Algorithm - ağırlıklı yönlendirilmemiş grafik için Minimum Yayılma Ağacı’nı (MST) bulma
• Böl ve Fethet - sorunu daha küçük parçalara bölün ve sonra bu parçaları çözün
  • B Binary Search
  • B Tower of Hanoi
  • B Pascal’s Triangle
  • B Euclidean Algorithm - calculate the Greatest Common Divisor (GCD)
  • B Merge Sort
  • B Quicksort
  • B Tree Depth-First Search (DFS)
  • B Graph Depth-First Search (DFS)
  • B Jump Game
  • B Fast Powering
  • A Permutations (tekrarlı ve tekrarsız)
  • A Combinations (tekrarlı ve tekrarsız)
• Dinamik Programlama - önceden bulunan alt çözümleri kullanarak bir çözüm oluşturmak
  • B Fibonacci Sayısı
  • B Jump Game
  • B Eşsiz Yol
  • B Rain Terraces - trapping rain water problem
  • B Recursive Staircase - zirveye ulaşmanın yollarının sayısını sayın
  • A Levenshtein Distance - iki sekans arasındaki minimum düzenleme mesafesi
  • A Longest Common Subsequence (LCS)
  • A Longest Common Substring
  • A Longest Increasing Subsequence
  • A Shortest Common Supersequence
  • A 0/1 Knapsack Problem
  • A Integer Partition
  • A Maximum Subarray
  • A Bellman-Ford Algorithm - tüm grafik köşelerine giden en kısa yolu bulmak
  • A Floyd-Warshall Algorithm - tüm köşe çiftleri arasındaki en kısa yolları bulun
  • A Regular Expression Matching
• Backtracking - brute forceye benzer, mümkün tüm sonuçları tara, ancak bir sonraki çözümü her ürettiğinizde test edersiniz tüm koşulları karşılıyorsa ve ancak o zaman sonraki çözümleri üretmeye devam edin. Aksi takdirde, geri dönün ve farklı bir çözüm arayın(?). Normally the DFS traversal of state-space is being used.
  • B Jump Game
  • B Unique Paths
  • B Power Set - all subsets of a set
  • A Hamiltonian Cycle - Her köşeyi tam olarak bir kez ziyaret edin
  • A N-Queens Problem
  • A Knight’s Tour
  • A Combination Sum - belirli toplamı oluşturan tüm kombinasyonları bulun
• Branch & Bound - remember the lowest-cost solution found at each stage of the backtracking search, and use the cost of the lowest-cost solution found so far as a lower bound on the cost of a least-cost solution to the problem, in order to discard partial solutions with costs larger than the lowest-cost solution found so far. Normally BFS traversal in combination with DFS traversal of state-space tree is being used.

Repository’in Kullanımı

Bütün dependencyleri kurun

npm install

ESLint’i başlatın

Bunu kodun kalitesini kontrol etmek amacı ile çalıştırabilirsin.

npm run lint

Bütün testleri çalıştır

npm test

Testleri ismine göre çalıştır

npm test -- 'LinkedList'

Deneme Alanı

data-structures ve algorithms içerisinde ./src/playground/playground.js yazarak ./src/playground/__test__/playground.test.js için test edebilirsin.

Ardından basitçe alttaki komutu girerek kodunun beklendiği gibi çalışıp çalışmadığını test edebilirsin:

npm test -- 'playground'

Yararlı Bilgiler

Referanslar

▶ Data Structures and Algorithms on YouTube

Big O Notation

• Big O notation *, algoritmaları, giriş boyutu büyüdükçe çalışma süresi veya alan gereksinimlerinin nasıl arttığına göre sınıflandırmak için kullanılır. Aşağıdaki grafikte, Big O gösteriminde belirtilen algoritmaların en yaygın büyüme sıralarını bulabilirsiniz.

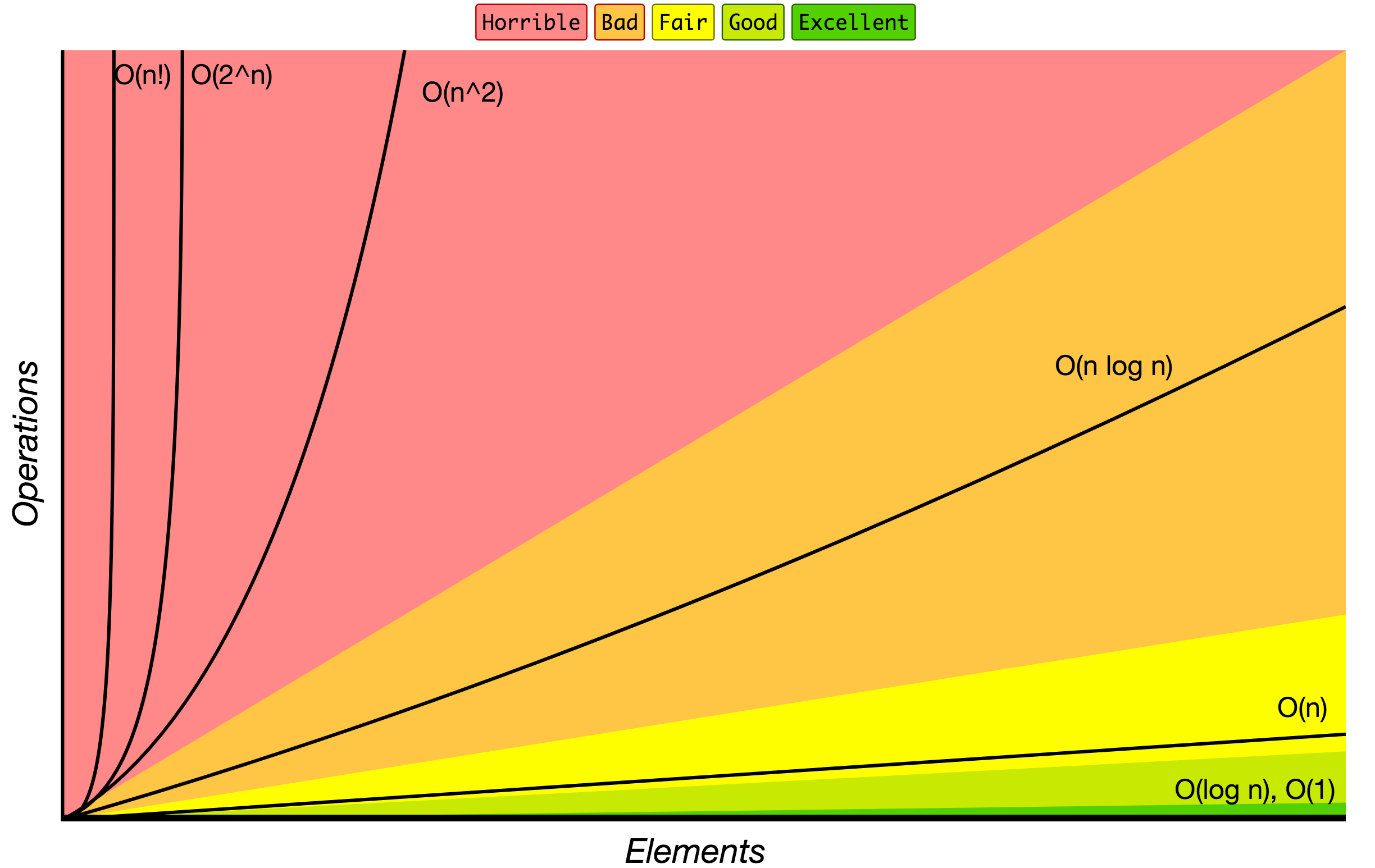
Kaynak: Big O Cheat Sheet.

Altta Big O notations ve farklı input boyutlarına karşın yapılmış performans karşılaştırması listelenmektedir.

Big O Notation	10 Element için hesaplama	100 Element için hesaplama	1000 Element için hesaplama
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

Veri Yapısı İşlem Karmaşıklığı

Veri Yapısı	Access	Search	Insertion	Deletion	Comments
Dizi	1	n	n	n
Yığın	n	n	1	1
Sıralı	n	n	1	1
Bağlantılı Liste	n	n	1	n
Yığın Tablo	-	n	n	n	Kusursuz hash fonksiyonu durumunda sonuç O(1)
İkili Arama Ağacı	n	n	n	n	In case of balanced tree costs would be O(log(n))
B-Tree	log(n)	log(n)	log(n)	log(n)
Red-Black Tree	log(n)	log(n)	log(n)	log(n)
AVL Tree	log(n)	log(n)	log(n)	log(n)
Bloom Filter	-	1	1	-	Arama esnasında yanlış sonuçlar çıkabilir

Dizi Sıralama Algoritmaları Karmaşıklığı

İsim	En İyi	Ortalama	En Kötü	Hafıza	Kararlı	Yorumlar
Bubble sort	n	n2	n2	1	Evet
Insertion sort	n	n2	n2	1	Evet
Selection sort	n2	n2	n2	1	Hayır
Heap sort	n log(n)	n log(n)	n log(n)	1	Hayır
Merge sort	n log(n)	n log(n)	n log(n)	n	Evet
Quick sort	n log(n)	n log(n)	n2	log(n)	Hayır	Hızlı sıralama genellikle O(log(n)) yığın alanıyla yapılır
Shell sort	n log(n)	depends on gap sequence	n (log(n))2	1	Hayır
Counting sort	n + r	n + r	n + r	n + r	Evet	r - dizideki en büyük sayı
Radix sort	n * k	n * k	n * k	n + k	Evet	k - en uzun key’in uzunluğu

Projeyi Destekleme

Bu projeyi buradan destekleyebilirsiniz ❤️️ GitHub veya ❤️️ Patreon.

This site is open source. Improve this page.